pinpax.blogg.se - How to match a z score of 6 on the standard normal table

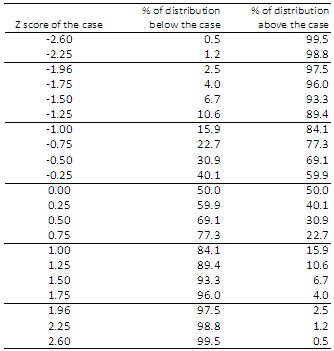
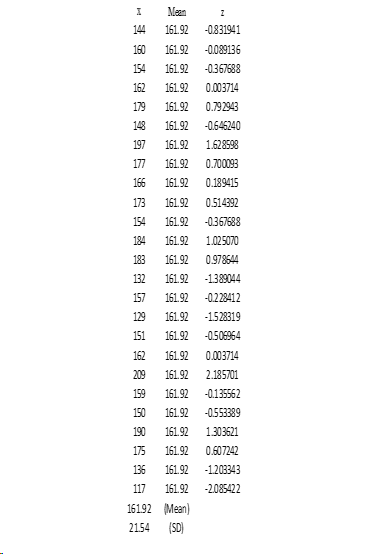
The area under the part of a normal curve that lies within 1 standard deviation of the mean is approximately 0.68 or 68% within two standard deviations, about 0.95 or 95% and within 3 standard deviations, about 0.997 or 99.7%.This fact may seem unusual, since the curve never touches the x-axis, but once can prove it mathematically by using claculus. The total area under a normal distribution curve is equal to 1.00 or 100%.Theoretically the curve never touches the x-axis but it gets increasingly closer.The curve is continuous that is there are no gaps or holes For each value of x, there is a corresponding value of y.

The curve is symmetric about the mean, which is equivalent to saying that its shape is the same on both sides of a vertical line passing through the center.

A normal distribution curve is unimodal.

The mean, median, and mode are equal and are located at the center of the distribution.

You will need to enter population mean, standard deviation of the distribution (for.

a continuous symmetric, bell-shaped distribution of a variable This online Z score calculator tool will calculate a Z score value.